Sebelum kita belajar lebih lanjut lagi tentang Binary Search Tree atau sering disingkat BST. Bapak Henry Chong , dosen saya , mereview ulang apa itu binary tree.
Jadi, Binary Tree adalah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimaldua subtree dan kedua subtree tersebut harus terpisah. Sesuai dengan definisi tersebut
tiap node dalam binary tree hanya boleh memiliki paling banyak dua child.
Berikut adalah contoh dari Binary Tree :
Binary Search Tree adalah struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap clild node sebelah kiri selalu lebih kecil nilainya dari pada root node. Begitu pula sebaliknya, setiap child node sebelah kanan selalu lebih besar nilainya daripada root node. BST maksimal mempunyai anak hanya 2 node.
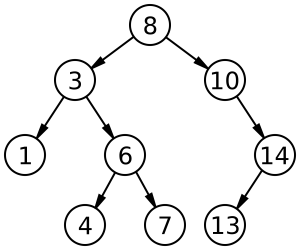
Dosen saya menjelaskan tujuan dari binary search tree(BST) adalah untuk memudahkan program dalam melakukan proses pencarian. Jika kita ingin menghapus node di angka 8 maka kita akan menggantinya dengan angka yang paling besar di leaf kiri atau dengan angka paling kecil di leaf kanan.
Ini adalah graf, dan ini bukan binary search tree, karena rootnya (angka 2) mempunya tiga node ,yaitu 1,4,3 yang berarti ia mempunyai loopingan.
Syarat Aturan Dari Binary Search Tree :
- Setiap child node sebelah kiri harus lebih kecil nilainya daripada root nodenya.
- Setiap child node sebelah kanan harus lebih besar nilainya daripada root nodenya.
Lalu, ada 3 jenis cara untuk melakukan penelusuran data (traversal) pada BST :
- PreOrder : Print data, Cek ke kiri, Cek ke kanan
- InOrder : Cek ke kiri, print data, Cek ke kanan
- Post Order :Cek ke kiri, Cek ke kanan, print data
Berikut saya sarankan untuk membuka video ini untuk mendalami ilmu yang lebih dalam lagi.
Berikut saya lampirkan codingan tentang BST :
#include<iostream>
#include<cstdlib>
using namespace std;
class BinarySearchTree{
private:
struct node{
node* left;
node* right;
int data;
};
node* root;
public:
BinarySearchTree(){
root = NULL;
}
bool isEmpty() const {return root==NULL;}
struct node* newNode(int data){
struct node* node = new(struct node);
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
struct node* insert(struct node* node, int data){
if(node == NULL){
return(newNode(data));
}
else{
if (data <= node->data) node->left = insert(node->left, data);
else node->right = insert(node->right, data);
return(node);
}
}
void insert(int data){
if(isEmpty()){
root = newNode(data);
}else{
insert(root,data);
}
}
void printTree(struct node* node){
if(node == NULL)return;
/*InOrder
printTree(node->left);
cout<<" "<<node->data;
printTree(node->right);
/*PreOrder
cout<<" "<<node->data;
printTree(node->left);
printTree(node->right);*/
/*PostOrder
printTree(node->left);
printTree(node->right);
cout<<" "<<node->data;*/
}
void callPrintTree(){
printTree(root);
}
int callLookup(int target){
return lookup(root,target);
}
int lookup(struct node* node,int target){
if(node==NULL) return 0;
if(node->data == target)return 1;
else{
if(target < node->data)
return lookup(node->left,target);
else
return lookup(node->right,target);
}
}
int callMin(){
return min(root);
}
int min(struct node* node){
if(node->left==NULL) return node->data;
else return min(node->left);
}
int callMax(){
return max(root);
}
int max(struct node* node){
if(node->right==NULL)return node->data;
else return max(node->right);
}
int callDept(){
return dept(root);
}
int dept(struct node* node){
if(node == NULL) return 0;
else{
int l = dept(node->left);
int r = dept(node->right);
if(l < r) return 1 + r;
else return 1 + l;
}
}
};
int main(){
BinarySearchTree b;
b.insert(5);
b.insert(3);
b.insert(9);
b.insert(1);
b.insert(4);
b.insert(6);
//b.callPrintTree();
cout<<b.callLookup(4)<<endl; //output : 1
cout<<b.callLookup(2)<<endl; //output : 0
cout<<b.callMin()<<endl; //output : 1
cout<<b.callMax()<<endl; //output : 9
cout<<b.callDept()<<endl; // output : 3
getchar();
return 0;}
#include<cstdlib>
using namespace std;
class BinarySearchTree{
private:
struct node{
node* left;
node* right;
int data;
};
node* root;
public:
BinarySearchTree(){
root = NULL;
}
bool isEmpty() const {return root==NULL;}
struct node* newNode(int data){
struct node* node = new(struct node);
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
struct node* insert(struct node* node, int data){
if(node == NULL){
return(newNode(data));
}
else{
if (data <= node->data) node->left = insert(node->left, data);
else node->right = insert(node->right, data);
return(node);
}
}
void insert(int data){
if(isEmpty()){
root = newNode(data);
}else{
insert(root,data);
}
}
void printTree(struct node* node){
if(node == NULL)return;
/*InOrder
printTree(node->left);
cout<<" "<<node->data;
printTree(node->right);
/*PreOrder
cout<<" "<<node->data;
printTree(node->left);
printTree(node->right);*/
/*PostOrder
printTree(node->left);
printTree(node->right);
cout<<" "<<node->data;*/
}
void callPrintTree(){
printTree(root);
}
int callLookup(int target){
return lookup(root,target);
}
int lookup(struct node* node,int target){
if(node==NULL) return 0;
if(node->data == target)return 1;
else{
if(target < node->data)
return lookup(node->left,target);
else
return lookup(node->right,target);
}
}
int callMin(){
return min(root);
}
int min(struct node* node){
if(node->left==NULL) return node->data;
else return min(node->left);
}
int callMax(){
return max(root);
}
int max(struct node* node){
if(node->right==NULL)return node->data;
else return max(node->right);
}
int callDept(){
return dept(root);
}
int dept(struct node* node){
if(node == NULL) return 0;
else{
int l = dept(node->left);
int r = dept(node->right);
if(l < r) return 1 + r;
else return 1 + l;
}
}
};
int main(){
BinarySearchTree b;
b.insert(5);
b.insert(3);
b.insert(9);
b.insert(1);
b.insert(4);
b.insert(6);
//b.callPrintTree();
cout<<b.callLookup(4)<<endl; //output : 1
cout<<b.callLookup(2)<<endl; //output : 0
cout<<b.callMin()<<endl; //output : 1
cout<<b.callMax()<<endl; //output : 9
cout<<b.callDept()<<endl; // output : 3
getchar();
return 0;}
Yoel Jordanio Imanuel
2101632055







